Las construcciones geométricas adquirieron gran importancia, tanto en Grecia como en India, en relación con rituales religiosos para la construcción de altares con forma y magnitud dadas. En Grecia, esto llevó al famoso problema de la duplicación del cubo, mientras que en India, lo importante en los altares era el área y no el volumen. En ambos casos, un paso esencial era resolver el siguiente problema: hallar un cuadrado que tenga la misma área que un rectángulo dado. Mientras los griegos lo resolvieron usando fundamentalmente la construcción del medio proporcional entre segmentos, los indios utilizaron el teorema de Pitágoras para resolverlo, en alrededor del año -600, cuando difícilmente podían haber sido influenciados por los griegos, lo que nos habla de algún origen común.
Los problemas aparecen en los textos; así encontramos en textos griegos, por ejemplo, un diálogo donde los delianos consultan al oráculo para liberarse de una plaga. El Dios (Apolo) les contesta a través del oráculo que deben construir un altar que tenga el doble de tamaño que el actual, pero la misma forma. La resolución de problemas de este tipo utilizando sólo la regla y el compás (aunque los mismos griegos no vacilaron en construir y utilizar otros instrumentos) preocupó a los matemáticos durante siglos. Los llamados "problemas clásicos", como la duplicación del cubo, la trisección del ángulo, la construcción del heptágono regular y la cuadratura del círculo, fueron satisfactoriamente resueltos (de hecho se probó la imposibilidad de realizar cualquiera de ellos) recién en los siglos XVIII y XIX.
 |
| Los cubos de Platón. |
Lamina de dibujo Nº 03 Construcciones Geométricas "Triángulos/Cuadriláteros"
Estimado participante, para esta lamina ya tienes conocimiento de como utilizar adecuadamente los materiales e instrumentos de trabajo, ademas de haber realizado los ejercicios para construcción de lineas paralelas, perpendiculares y divisiones de ángulos.
Al fijar la lamina cuyo formato es DIN-A3 sobre la superficie de trabajo deberás dividir el area en 8 partes iguales. Recuerda eluso adeacuado de lineas y de los rótulos al desarrollar e identificar los ejercicios. Trabajaras en centímetros.
Ejercicio 1. Construir un triangulo equilátero, dado un lado AB 0,05m.
Ejercicio 2. Construir un triangulo isosceles, dados dos lados Y 0,065m X 0,055m
Ejercicio 3. Construir un triangulo rectangulo, dado el lado AB 0,055m
Ejercicio 4. Construir un tiangulo equilatero, dada la altura h 0,06m
Ejercicio 5. Construir un cuadrado, dado el lado AB 52,5 mm
Ejercicio 6. Construir un cuadrado, dada la diagonal L 70 mm
Ejercicio 7. Construir un rectangulo, dada la base y el lado R 65 mm S 40 mm
Ejercicio 8. Construir un paralelogramo, dado los lados y un angulo R 60mm S 40mm y el angulo MON 47º.
Lamina de dibujo Nº 04 Construcciones Geométricas "Polígonos"
Una vez finalizada la Lamina anterior (Triangulos/Cuadrilateros), fija sobre la superficie de trabajo una lamina la cual deberas dividir en 06 seis partes iguales; recuerda que en los marcos y procedimientos debes utilizar de forma correcta los materiales e instrumentos de trabajo, ademas de rotular adecuadamente tu trabajo. Trabajaras en metros utilizando el escalimetro en la escala indicada.
Lamina de dibujo Nº 04 Construcciones Geométricas "Polígonos"
Una vez finalizada la Lamina anterior (Triangulos/Cuadrilateros), fija sobre la superficie de trabajo una lamina la cual deberas dividir en 06 seis partes iguales; recuerda que en los marcos y procedimientos debes utilizar de forma correcta los materiales e instrumentos de trabajo, ademas de rotular adecuadamente tu trabajo. Trabajaras en metros utilizando el escalimetro en la escala indicada.
Ejercicio 1. Construir un pentágono, dado un lado AB 1,20 m. Esc: 1/20
Ejercicio 2. Construir un hexágono, dados un lado AB 2,5 m. Esc: 1/50
Ejercicio 3. Construir un Heptágono, dado el lado AB 3 m. Esc: 1/100
Ejercicio 4. Dividir una circunferencia cuyo radio es de R= 50 m en nueve partes iguales, e inscribir el eneágono. Esc: 1/1250
Ejercicio 5. Dividir una circunferencia cuyo diámetro es de D=2 m en doce partes iguales, e inscribir e dodecágono. Esc: 1/25
Ejercicio 6. Dividir una circunferencia cuyo diametro es D= 3 m en quince partes iguales, e inscribir un pentadecagono. Esc: 1/75



 , en un polígono de
, en un polígono de  lados.
lados.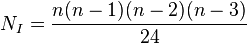 , en un polígono de
, en un polígono de 
 o
o  .
.