Polígono

En geometría, un polígono es una figura plana compuesta por una secuencia limitada de segmentos rectos consecutivos que cierran una región en el plano. Estos segmentos son llamados lados, y los puntos en que se interceptan se llaman vértices. El interior del polígono es llamado área. El polígono es el caso bidimensional del politopo, figura geométrica general definida para cualquier número de dimensiones. A su vez, un politopo de tres dimensiones se denominapoliedro, y de cuatro dimensiones se denomina polícoro.

Polígonos

El origen de la palabra poligono, deriva del griego antiguo πολύγωνος (polúgonos), a su vez formado por πολύ (polú) ‘muchos’ y γωνία (gōnía) ‘ángulo’, aunque hoy en día los polígonos son usualmente entendidos por el número de sus lados. 

Elementos de un Polígono.

En un polígono se pueden distinguir los siguientes elementos geométricos:

• Lado (L): es cada uno de los segmentos que conforman el polígono.
• Vértice (V): es el punto de intersección (punto de unión) de dos lados consecutivos.
• Diagonal (D): es el segmento que une dos vértices no consecutivos.
• Perímetro (P): es la suma de las longitudes de todos los lados del polígono.
• Semiperímetro (SP): es la mitad del perímetro.
• Ángulo interior (AI): es el ángulo formado, internamente al polígono, por dos lados consecutivos.
• Ángulo exterior (AE): es el ángulo formado, externamente al polígono, por un lado y la prolongación de un lado consecutivo.
• Interior de un polígono es el conjunto de todos los puntos que están en el interior de la región que delimita dicho polígono. El interior es un abierto del plano.
• Exterior de un polígono es el conjunto de los puntos que no están en la poligonal (frontera) ni en el interior. El exterior es un abierto del plano.
• Si el complemento (exterior) de una región poligonal es inconexo, este constará de varios fragmentos conexos llamados componentes. Uno y solo uno de los componente es ilimitado; todos los demás son limitados, a estos últimos se llaman huecos. Cada hueco con su frontera es un polígono.

Partes del Polígono

En un polígono regular se puede distinguir, además:

• Centro (C): es el punto equidistante de todos los vértices y lados.
• Ángulo central (AC): es el ángulo formado por dos segmentos de recta que parten del centro a los extremos de un lado.
• Apotema (a): es el segmento que une el centro del polígono con el centro de un lado; es perpendicular a dicho lado.
• Diagonales totales , en un polígono de  lados.
• Intersecciones de diagonales 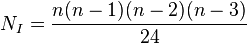, en un polígono de  vértices.
• Todo polígono regular de n lados, puede ser descompuesto en un conjunto ordenado de n-2 triángulos, con un vértice común y la suma de las áreas de los triángulos sea igual al área del polígono.

Partes del Polígono

Clasificación de los polígonos según su contorno:

Según las propiedades que cumpla el contorno del polígono, es posible realizar las siguientes clasificaciones.

• Simple, si ningún par de aristas no consecutivas se corta. Equivalentemente, su frontera tiene un solo contorno.
• Complejo o Cruzado , si dos de sus aristas no consecutivas se intersecan.
• Convexo, si todo segmento que une dos puntos cualesquiera del contorno del polígono yace en el interior de este. Todo polígono simple y con todos sus ángulos internos menores que 180º es convexo.
• No convexo, si existe un segmento entre dos puntos de la frontera del polígono que sale al exterior del mismo. O si existe una recta capaz de cortar el polígono en más de dos puntos.
• Cóncavo, si es un polígono simple y no convexo.
• Equilátero, si tiene todos sus lados de la misma longitud.
• Equiángulo, si tiene todos sus ángulos interiores iguales.
• Regular, si es equilátero y equiángulo a la vez.
• Irregular, si no es regular. Es decir, si no es equilátero o equiángulo.
• Cíclico, si existe una circunferencia que pasa por todos los vértices del polígono. Todos los polígonos regulares son cíclicos.
• Ortogonal o Isotético, si todos sus lados son paralelos a los ejes cartesianos  o .
• Alabeado, si sus lados no están en el mismo plano.
• Estrellado, si se construye a partir de trazar diagonales en polígonos regulares. Se obtienen diferentes construcciones dependiendo de la unión de los vértices: de dos en dos, de tres en tres, etc.
• Reticular es simple y, al representarlo en un reticulado, cada vértice yace exactamente en un vértice de cuadrado unitario del reticulado (en este caso funciona la fórmula de Pick).

Clasificación de los polígonos según su numero de lados:

Los polígonos tienen un nombre especial para designar el número de lados del mismo. Los nombres más comunes son los siguientes:

Nombre	n.º lados
trígono o triángulo	3
tetrágono, cuadrángulo o cuadrilátero	4
pentágono	5
hexágono	6
heptágono	7
octógono u octágono	8
eneágono o nonágono	9
decágono	10
endecágono o undecágono	11
dodecágono	12
tridecágono	13
tetradecágono	14
pentadecágono o pentedecágono	15
hexadecágono	16
heptadecágono	17
octodecágono u octadecágono	18
eneadecágono o nonadecágono	19
isodecágono o icoságono	20
triacontágono	30
tetracontágono	40
pentacontágono	50
hexacontágono	60
heptacontágono	70
octocontágono u octacontágono	80
eneacontágono o nonacontágono	90
hectágono	100
chiliágono	1000
miriágono	10000
decemiriágono	100000
hectamiriágono o megágono	1000000
apeirógono	∞